It’s Elemental: Accurate Analysis of Earth‘s Core with Molecular Dynamics Simulation
Updatetime:2012-12-31From:
【Enlarge】【Reduce】
Accurately determining the relative percentages of the elements comprising the Earth's core and mantle which formed early – that is, within 30 Ma (megaannum, or million years) after the solar system itself formed – are extremely difficult for a range of reason, not the least of which is that direct measurement-is impossible. In particular, elements lighter than iron are of great interest due to their potential role in the Earth's so-called core density deficit. Moreover, carbon, among the light element candidates, also affects how siderophile and chalcophile (literally, iron-loving and sulfur-loving, respectively) elements partition between metal and silicate – which in turn has an impact on how these elements are distributed in the core and mantle. Previously, core carbon estimates varied by a factor as high as 20, resulting not only from assumptions and methodology, but also, significantly, because the carbon metal–silicate partition coefficient unknown. Recently, however, scientists at the Chinese Academy of Sciences, Beijing and the University of California, Davis, used two-phase first-principles molecular dynamics – an accurate atomistic simulation method combining a quantum mechanical description of electrons with a classical description of atomic nuclei – to accurately derive the partition coefficient of carbon and other light elements between liquid iron and silicate melt.
 |
|
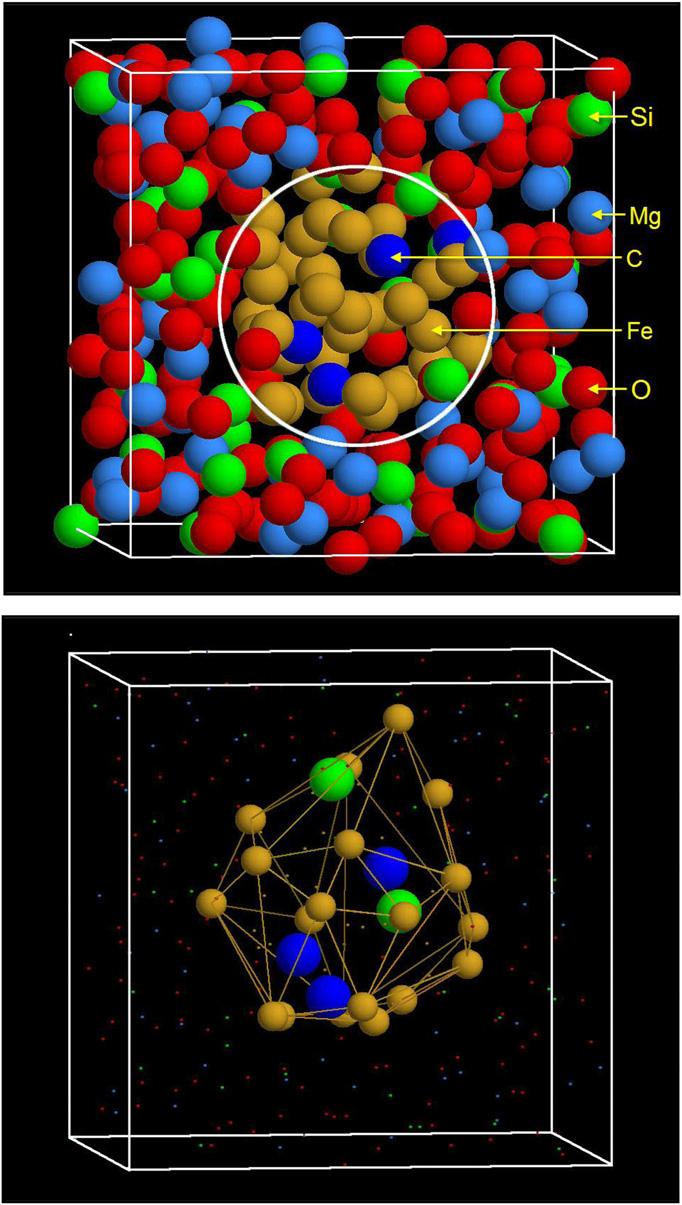
(Upper) Snapshot of atomic configuration in the simulation cell after the center of mass of the Fe cluster is moved to the center of the simulation cell and all of the atoms are moved accordingly by using the periodic conditions of the simulation cell. The encircled area marks the liquid metal phase domain and the surrounding area is the silicate melt domain. (Lower) The constructed alpha shape of the Fe cluster showing Fe atoms on the surface of the alpha shape and the Si and C atoms enclosed in the alpha shape. Copyright C PNAS, doi:10.1073/pnas.1203826109 |
Prof. Qing-Zhu Yin and Dr. Yigang Zhang (at the University of California, Davis and the Chinese Academy of Sciences, Beijing, respectively) discussed their research with Phys.org. "Our major challenge in using two-phase first-principles molecular dynamics to derive the metal–silicate partition coefficient of carbon from liquid iron and silicate melt," says Zhang, "was that we had to first develop our methodology, since it didn't previously exist."
"Moreover," Yin adds, "we didn't have any templates to work with – so we had to start from scratch, and then had to test to see if the method really worked." Yin and Zhang did this by comparing it with available experimental or observational data. "After all," Yin continues, "we're using only some 260 atoms within the computer to simulate the entire Earth, which contains some 47 orders of magnitude more atoms."
Another challenge the scientists faced was evaluating their results in relation to previous estimates of carbon content divergence. "Our primary results are the partition coefficients for carbon and a suite of other light elements – namely how carbon and other light elements are distributed between molten metal and molten silicate under extreme pressure and temperature of magma oceans" notes Zhang. "Once we had this partition coefficient computed for each element, it was straightforward to derive carbon content of the Earth core."
To perform this derivation, the researchers needed the carbon content of the entire Earth or of the Earth's mantle. "There were some estimates from meteoritics and cosmochemistry using chondrites as the building blocks for the entire Earth, and the direct observational data from the Earth's mantle from geochemistry," says Yin. Previous attempts to deriving carbon content of the Earth core assume either that carbon is supersaturated during the Earth's accretion process, or that carbon is the only light element in the Earth core – both of which tends to give higher values. "The key to our solution," Yin points out, "was calculating the partition coefficient from first principles, since no experimental data exist for carbon solubility in liquid iron coexisting with silicate melt at carbon under-saturated condition. This highlights the technical difficulties to obtain experimental data for carbon, which makes our theoretical approach particularly valuable to fill in the niche in our knowledge gap."
In addition, applying this method to determine the partition coefficients of nitrogen, hydrogen, helium, phosphorus, magnesium, oxygen, and silicon also presented more challenges. "The method is most suitable for elements with a partition coefficient close to 1 between metal and silicate" said Zhang.
For strongly siderophile or strongly lithophile (rock-loving) elements, where the partition coefficients are either extremely large, or extremely small, their results tended to have larger uncertainties. "To overcome this problem," notes Yin, "we needed a large system size – that is, a much larger number of atoms – to compute more precise partition coefficients. However, computation of such a large system is unrealistically expensive and time-consuming with presently available computing power."
Finally, Yin and Zhang had to infer core carbon content by combining the derived partition coefficient with the composition of the bulk Earth or the primitive mantle. "In the case of carbon, our computed partition coefficient has ~30% uncertainty. However, the factor of seven carbon content of the Earth's core – that is, 0.1-0.7% - is governed primarily by the uncertainties with the current estimates of the bulk Earth or bulk silicate Earth mantle content of the carbon" said Yin, "we need independent constraints to narrow this down. If we can, the light element budget could be even more precisely constrained"
In addressing these challenges, Yin adds, their key insight was that they needed an entire suite of light elements – including oxygen, silicon, sulfur, carbon, phosphorus, magnesium, hydrogen, helium, and nitrogen – to account for the well-known core density deficit problem. "Any single elements would not do it. Although the core is the largest carbon reservoir inside the Earth, the carbon content of 0.1-0.7% would not be able to account for the core density deficit. As opposed to silicon, oxygen and sulfur, which are likely the three major light elements contents in the Earth's core, carbon is not even a major player."
In terms of innovative techniques, the team used computational geometry in calculating compositions of metal and silicate phases. "We also ran very lengthy simulations, allowing the system size limit to be overcome and leveraged," notes Zhang. "Each run takes about three months, and with a total of 24 runs reported in the paper, it took 72 months of intensive computation to complete the analyses."
Yin and Zhang are also developing other innovations to enhance the current experimental design. "The system we developed so far is composed of two liquids," Zhang explains. "We're now trying to design a new system where one of the phases is solid." This will allow them to simulate and analyze a range of additional situations – including, Yin illustrates, the Earth's solid inner core and liquid outer core, how the elements are redistributed when the solid inner core crystallizes from the liquid outer core, or conditions in the magma ocean when portions of silicate Earth mantle was not fully molten. "However, this will be more challenging," Zhang points out, "because the system will be more difficult to manipulate. Another challenge is that atoms in solid diffuse slowly so the simulations consume even more time and thus require more patience."
Beyond that, there are many planned next steps in the team's research. "There's so much more to do," says Yin. "So far the computation was largely simulating the static pressure and temperature condition inside the Earth at the base of the magma ocean. However, during the late, giant impact stages of terrestrial planet formation, both pressure and temperature could have been much higher but for much shorter period of time in that violent situation. While it would be extremely difficult to design experiments to mimic such conditions in laboratories, we can do so in computer simulations." Instead of 125 GPa (gigapascals, a measure of stiffness or tensile strength of materials) at a temperature of 3000K (4940° F), for example, they could analyze more extreme conditions of 500-1000 GPa at 5000-7000K. "The energy involved in the late giant impact stage is enough to make the proto-Earth glow like a low mass star for a brief period of time. We want to simulate a more realistic condition that was likely to have occurred during the Earth's formation."
"Using the new design where one of the phases will be solid, we're planning to do element partition between solid and liquid iron," Zhang notes. "This aims at studying the compositional difference between Earth's solid inner core and liquid outer core, which will give us further insight on the core composition." Yin adds that while they don't know whether the new methods will be successful, they're cautiously optimistic.
Yin expands on their study suggests that nitrogen retention occurs in a mantle phase instead of in the core. "Among the light elements investigated in our work, nitrogen has the lowest content in the Earth's core, and also gives the largest deviation among the different estimates. If our high-end estimate is correct, our calculation agrees with geochemical mass balance arguments within a factor of 2 (36-75 ppm). However, nitrogen content in the Earth's core could be as low as 3-4 ppm. The lower estimates critically depend on the estimates of nitrogen content of the Earth's mantle. If there are regions of the Earth mantle not represented by the mantle rocks in hand – that is, a hidden reservoir – our estimates of core nitrogen would be affected accordingly, and thus would be too low. If both our calculated nitrogen partition coefficient (1.8±0.2) and the Earth's mantle nitrogen estimates are correct, then the higher 36-75 ppm is due to overestimates nitrogen in the Earth as a whole." This would suggest that the Earth building blocks never had that much nitrogen to begin with. "At this point," Yin acknowledges, "we can't rule out either possibility."
Zhang also comments on another of their work's findings – namely, that partitioning experiments for siderophile elements using carbon as a sample encapsulating material significantly impact the behavior of these elements. "This is based on previously published experimental work by others, including Wood and Halliday1. It was shown that with carbon capsules, the lead content in the metal phase drops, but with a magnesium capsule, the lead content in the metal phase increases."
The scientists also see possibilities of their findings being applied to other areas or research. "Our goal is to use light element contents in the Earth's metallic core to probe the physicochemical conditions that existed during Earth's formation," says Yin. "The association of light elements, such as silicon and oxygen, associated with metal had to be a planetary-scale phenomenon." In iron meteorites, which are thought to come from cores of smaller asteroids, there's virtually no silicon and oxygen associated with the metal.
"Clearly one needs higher pressure and temperature to squeeze silicon and oxygen into the metal," Yin explains. "Given the amount of light element content in the core, we'd like to know the degree of chemical equilibration between silicate mantle and metallic core during the Earth accretion processes. Knowing this could help constrain the timing of the Moon forming giant impact, which marks the birth of a fully grown proto-Earth. In addition, our computational method could also be applied to other planets such to Mercury, Venus and Mars, which we plan to investigate in the near future."
More information: Carbon and other light element contents in the Earth's core based on first-principles molecular dynamics, PNAS November 27, 2012 vol. 109 no. 48 19579-19583, doi:10.1073/pnas.1203826109 (Phys.org)
Appendix




