Water in the soils is commonly called soil water. The state variation and phase transition of non-uniform water in soils play an important role in hydrothermal process simulation in cold regions, the formation and decomposition of hydrates, exploring water and ice in Moon, and others changing questions related to aqueous interfaces.  

Recently, the charactering of soil water state got increasingly focused on in soil science, but there still exists poorly understanding in its non-uniform nature.  

Researchers from the Northwest Institute of Eco-Environment and Resources of the Chinese Academy of Sciences (CAS) recently tried to propose a theory framework to further characterize the non-uniform nature of soil water and its phase transition dynamics.  

They introduced the static and dynamic theory methods of non-uniform water based on diffuse interface model (Fig. 1) to analyze non-uniform water state dynamics and water density and the pore water pressure.

Result clarifies the concepts of pore water state, pore water pressure and matric potential in classical soil mechanics.

The researchers also proposed that the phase transition theory of non-uniform water was proposed and found the generalized Clausius-Clapeyron equation (GCCE) is consistent with Clapeyron equation in nature (Fig. 2). 

Furthermore, the study shows that spatial non-uniform of interface water and its phase transition have a competitive advantage for key issues such as spatially non-uniform of soil-water density, questions of GCCE, pressure melting, promoting effect of substrates on hydrate formation and others.  

These results highlight the role of substrate-water unit in soil science and provide a theory basis for engineering and environmental sciences relative to frozen soil. 

Relevant results have been published in Advances in Colloid and Interface Science entitled “Spatial state distribution and phase transition of non-uniform water in soils: Implications for engineering and environmental sciences”. This research was supported by grants from the National Natural Science Foundation of China (no. 41501072). 

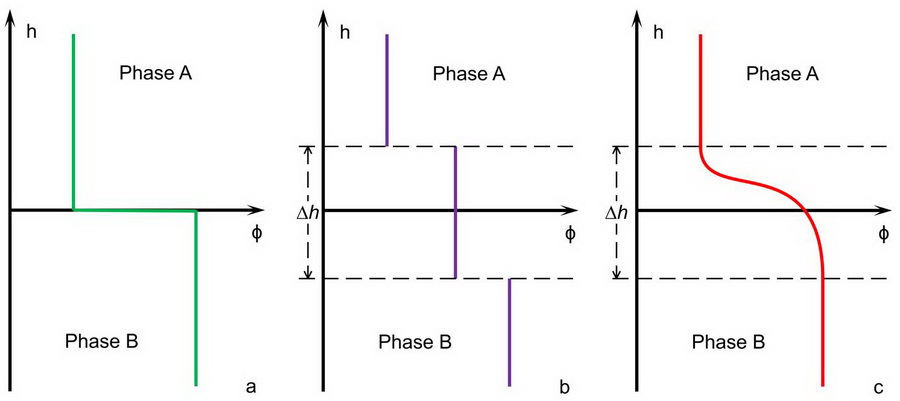
Fig. 1. The abstracted interface models between phase A and phase B. a: the sharp Gibbs interface model; b: the uniform interface model; c: the diffuse interface model. ？h is the interface thickness. Φ is the order parameter in the interface, which is a function of location h. (Image by ZHANG Lianhai) 

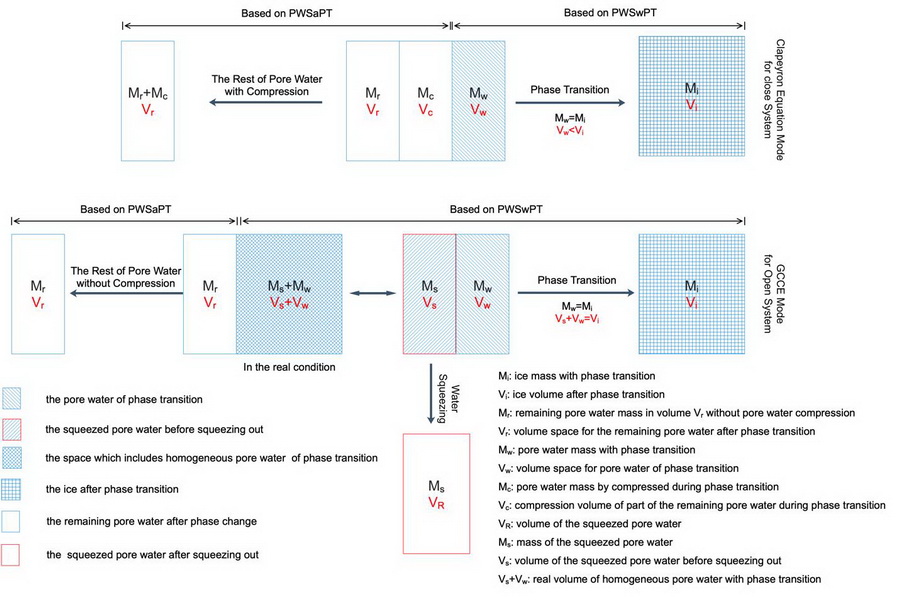
Fig. 2. The schematic diagram on two different phase transition modes. The blue cell and the blank cell present the phase transition volume space (PWSwPT) and the rest of pore water unassociated with but affected by phase transition (PWSaPT), respectively. The cell size denotes the pore water volume associated with relevant process. In the Clapeyron mode, the specific volume of water is less than that of ice due to constant mass (Mi = Mw) and changed volume (Vw < Vi) during phase transition, as shown in Eq. (35). In the GCCE mode, the effective volume of water is equal to that of ice due to constant mass (Mi = Mw) and constant volume (Vs + Vw = Vi) during phase transition, as shown in Eq. (38).  (Image by ZHANG Lianhai) 

Contact: 

ZHANG Lianhai 

E-mail: zhanglh@lzb.ac.cn 

State Key Laboratory of Frozen Soil Engineering, Beilu'he Observation and Research Station on Tibet Plateau, Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences, Lanzhou, China.